Подавляющее большинство людей не знает, что такое Парадокс Близнецов. Точнее, люди только думают, что будто бы знают, что такое Парадокс Близнецов.
При этом под Парадоксом Близнецов эти люди понимают следующую ахинею. Будто бы, если один из близнецов останется на Земле, а другой улетит на несколько лет в космос и будет там летать со скоростью близкой к скорости света, то когда он прилетит обратно на Землю, то, якобы, он окажется моложе, чем его брат близнец.
К сожалению, этот миф распространяют не только писатели фантасты и сценаристы кинофильмов (к ним нет никаких претензий), но и авторы многих научно-популярных книг и научно-популярных телепередач. Вносят свою лепту в эту мифологию и неграмотные журналисты, которые время от времени сообщают, что-то типа того, что у какого-нибудь космонавта или летчика очень точные часы стали отставать на миллионные доли секунды, якобы, из-за того, что эти часы долго летали с большой скоростью.
Поэтому рассмотрим здесь подробно, что такое на самом деле Парадокс Близнецов, и рассмотрим кратко, почему близнец, вернувшийся из космического путешествия всегда будет такого же возраста, как и его оставшийся на Земле брат.
Реальный Парадокс Близнецов
Пусть два космических корабля A и B где-то в межгалактическом пространстве разлетаются друг от друга по прямой линии с одинаковыми неменяющимися по величине скоростями, но противоположно направленными. Пусть их скорости v0 будут достаточно близкими к скорости света. Скорость v0 отсчитывается относительно наблюдателя, который находится всё время в той точке, откуда разлетелись оба космических корабля.

В этом случае получается, что, с точки зрения наблюдателя, время в этих космических кораблях идет совершенно одинаково, но отличается от его времени тем, что оно замедляется. Если на его часах прошло время t0, то в каждом из этих космических кораблей прошло время t, которое связано со временем t0 формулой:
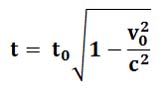
Здесь c, это скорость света. Если в этих ракетах сидят два брата близнеца, то у них будет один и тот же возраст относительно друг друга, так как время в их космических кораблях идет одинаково.
Например, если скорость v0 составляет 90% от скорости света (v0=0.9c), то получаем примерно t=0.4359t0. То есть наблюдатель считает, что, когда у него проходят одни сутки (24 часа), то в этих космических кораблях проходит примерно 10 часов 27 минут 42 секунды.
Все системы отсчета, которые движутся относительно друг друга равномерно и прямолинейно (инерциальные системы отсчета) являются равноправным. Поэтому мы можем считать наблюдателем человека, который летит в космическом корабле A.
Относительно этого наблюдателя в космическом корабле A, первый наблюдатель удаляется со скоростью v0. Значит, относительно наблюдателя в космическом корабле A, у первого наблюдателя время замедляется. Если, например, скорость v0 составляет 90% от скорости света (v0=0.9c), то получаем примерно t=0.4359t0. То есть наблюдатель в корабле A считает, что, когда у него проходят одни сутки (24 часа), то у первого наблюдателя проходит примерно 10 часов 27 минут 42 секунды.
А как с точки зрения наблюдателя из корабля A идет время в корабле B?
Для этого сначала надо посчитать скорость, с которой оба космических корабля разлетаются друг от друга. Для этого воспользуемся формулой сложения скоростей:
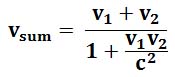
Например, если каждый космический корабль летит со скоростью 90% от скорости света (v0=0.9c), то получаем, что скорость v относительного разбегания кораблей A и B друг от друга будет примерно v=0.9945c. Подставляем эту скорость вместо скорости v0 в формулу для расчета времени и получаем, что время tB в космическом корабле B относительно времени tA в космическом корабле A будет tB=0.1047tA. Таким образом, наблюдатель в космическом корабле A считает, что, когда у него проходят одни сутки (24 часа), то на космическом корабле B проходит примерно 2 часов 30 минут 49 секунд.
Получается, что если в космических кораблях A и B сидят два брата близнеца, то с точки зрения первого наблюдателя возраст этих близнецов одинаковый. Но вот с точки зрения близнеца в корабле A, его брат в корабле B теперь стареет медленнее. Если, например, v0=0.9c, то его брат стареет примерно в 10 раз медленнее (tB=0.1047tA).Например, если им было ровно по 30 лет, когда стартовали космические корабли, то через 10 лет близнец в корабле A будет считать, что ему уже исполнилось ровно 40 лет, а его брату в корабле B еще только 31 год и 17 дней.
Понятно, что эта ситуация симметричная, поэтому точно также может рассуждать и близнец из корабля B про возраст своего брата в космическом корабле A. С точки зрения близнеца в корабле B, это, наоборот, у него идет время нормально, а у его брата в корабле A время идет примерно в 10 раз медленнее.
Вот в этом-то и заключается Парадокс Близнецов: Разница в возрасте близнецов существенно зависит от выбранной наблюдателем системы отсчета.
Именно так этот парадокс и был сформулирован первоначально. Никаких утверждений там никогда не было, про то, что, если один близнец остается на Земле, а другой полетит на долгие годы в космос с большой скорость, то, когда он вернется, то, якобы, он будет моложе своего оставшегося на Земле брата. Ничего подобного в этом Парадоксе Близнецов никогда не утверждалось.
Выбор системы отчета
Обратите внимание, что с помощью выбора системы отсчета мы можем сделать разницу в возрасте близнецов любой в некоторых пределах. Эти пределы зависят и от скорости наблюдателя и от скорости взаимного разлёта двух космических кораблей.
Уменьшение разницы в возрасте близнецов
Например, пусть имеется еще один наблюдатель, который постоянно находится на полпути от первого наблюдателя до корабля A. То есть он летит от первого наблюдателя за кораблем A со скоростью v2=v0/2 относительно первого наблюдателя. Если v0=0.9c, то, с точки зрения этого второго наблюдателя, время в корабле A немного отстает от его часов: tA=0.9473t2. А время в корабле B отстает от его часов более существенно: tB=0.2771t2. Получается, что относительно второго наблюдателя разница во времени в двух космических кораблях будет: tA-tB=0.6702t2.
Таким образом, скорость старения брата в корабле B составляет примерно 67.02% от скорости старения брата в корабле A. Если на старте им было ровно по 30 лет, то ровно через 10 лет по часам второго наблюдателя близнецу в корабле A исполнится 39 лет 5 месяцев 20 дней, а близнецу в корабле B исполнится только 32 года 9 месяцев 7 дней.
Эта разница составляет 6 лет 8 месяцев 12 дней. Обратите внимание, что эта разница меньше, чем посчитал разницу близнец в корабле A. Он насчитал разницу 8 лет 11 месяцев 13 дней. (Для простоты считаем в каждом месяце 30 дней.) Ведь он думает, что, когда ему исполнилось 40 лет, то его брату исполнилось только 31 год и 17 дней (см. предыдущий раздел).
Увеличение разницы в возрасте близнецов
Оказывается можно так выбрать систему отсчета, чтобы разница в возрасте между близнецами стала больше, чем считает близнец на космическом корабле A. Для этого третий наблюдатель должен лететь в том же направлении, как и корабль A, но с такой скоростью относительно первого наблюдателя, которая больше, чем скорость космического корабля A.
Например, если третий наблюдатель летит со скоростью v3=0.99c, то за 10 лет по часам третьего наблюдателя между близнецами набежит разница в возрасте 9 лет 8 месяцев 2 дня. На такой возраст близнец в космическом корабле A окажется старше своего брата в корабле B.
Максимальную разницу в возрасте близнецов можно получить в размере 9 лет 11 месяцев 25 дней. Это когда третий наблюдатель летит с очень-очень большой скоростью v3, которая очень-очень близкая к скорости света и отличается от скорости света на миллиардные доли процента.
А самую большую разницу в возрасте близнецов можно получить, если космические корабли A и B будут удаляться от первого наблюдателя, который находится точно между ними, со скоростями не v0=0.9c, а со скоростями очень близкими к скорости света. Чем больше будет их скорость v0, тем ближе разница в возрасте приблизится к 10 лет за 10 лет по часам третьего наблюдателя, который летит со скоростью больше или равной, чем скорость корабля A.
Относительность времени
Описанный здесь Парадокс Близнецов основан на относительности времени в Специальной Теории Относительности (СТО). Время зависит от выбора той или иной системы отсчета. Поэтому выбирая разные системы отсчета можно получить разные разницы во времени между другими системами отсчета.
Корректное сравнение часов
Понятно, что не может быть такого, чтобы близнецы были одновременно и одного возраста и разных возрастов. А если оба близнеца стали разных возрастов, то не может быть такого, чтобы одновременно один из близнецов был и старше и младше своего брата.
Ведь если человек живет не более 100 лет, то не может же быть, например, такой ситуации, когда первый близнец уже умер, а второй еще нет, и одновременно с этим, первый близнец еще жив, а второй уже умер. Это же не коты Шредингера, чтобы находиться одновременно в состоянии мертвого и живого.
Поэтому в СТО введено понятие корректного сравнения показания часов. Точнее, не часов, а времени. Ну, или часов, если под понятием часы понимать идеальный абсолютно точный прибор измерения времени.
Корректно сравнивать показания часов, только если эти часы находятся одновременно в одной и той же точке пространства и в одной и той же системе отсчета. Это самый простой вид формулировки принципа корректного сравнения часов.
Этот принцип корректного сравнения часов можно обобщить на случай неодновременного присутствия в одной и той же точке пространства с некоторой разницей во времени. А также этот принцип можно обобщить и на случай присутствия часов в разных точках пространства, и тогда сравнение показаний этих часов делается с учетом времени прохождения электромагнитного сигнала от одних часов к другими часам. Но мы рассматривать эти обобщения не будем. Нам достаточно и самой простой формулировки этого принципа.
Теперь понятно, что мы не можем корректно сравнивать возраст двух близнецов до тех пор, пока они снова не встретятся друг с другом. Причем под встречей близнецов понимается не просто пролёт двух ракет на скорости возле друг друга. Летящие мимо друг друга ракеты, это ведь разные системы отсчета.
Нужно, чтобы космические корабли остановились относительно друг друга. В этом случае уже можно сравнивать часы с учетом расстояния между кораблями и временем прохождения электромагнитного сигнала между ними. Но для приведенной выше простой формулировки корректного сравнения часов нужно, чтобы оба космических корабля одновременно прибыли в одно и то же место в космосе. Ну, проще говоря, чтобы близнецы реально встретились друг с другом.
Ограничения СТО
Для этого нужно, чтобы их космические корабли развернулись и полетели обратно на встречу друг другу. (Или просто остановились, как требует обобщенный принцип сравнения часов.)
Но рассмотреть этот процесс в рамках СТО невозможно. Дело в том, что СТО рассматривает только равномерные прямолинейные движения. Торможение космического корабля и/или разворот космического корабля, это изменение скорости корабля, то есть движение с ускорением. СТО не рассматривает такие движения.
Поэтому в рамках СТО Парадокс Близнецов не может быть решен.
Решение Парадокса Близнецов в рамках ОТО
Движения с ускорениями рассматривает не СТО, а ОТО (Общая Теория Относительности). В рамках ОТО Парадокс Близнецов был успешно решен.
Рассмотрим двух близнецов. Чтобы упростить рассмотрение будем всегда находиться в системе отсчета, связанной с одним из близнецов. Центр этой системы отсчета поместим прямо в то место, где находится первый близнец. Нам совершенно не важно, где находится этот первый близнец, в ракете или неподвижно на Земле в гравитационном поле Земли или он находится в свободном падении на Землю (на другую планету, на звезду, на черную дыру и т.д.). Нам не важно, как меняется его ускорение или гравитационное поле, которое его окружает.
Первоначально второй близнец находится рядом с первым близнецом. Но в какой-то момент он покидает своего брата и начинает летать по космосу. Он летает с самыми разными скоростями (не более скорости света, естественно) с любыми остановками относительно системы отсчета первого близнеца с самыми разными ускорениями по любым траекториям, которые могут в пространстве сколь угодно раз пересекаться. Траектория второго близнеца также может пересекать любые гравитационные поля (кроме тех, что находятся за горизонтом черной дыры, естественно, иначе рандеву братьев никогда не состоится).
Главное, чтобы, рано или поздно, траектория второго близнеца пришла в ту точку, где находится первый близнец, и скорость второго близнеца стала в той точке равной нулю. Теперь сравниваем возраст близнецов. Возраст близнецов будет совпадать. Ни один из двух близнецов не окажется старше или младше другого. Корректное сравнение часов показывает, что показания часов абсолютно точно совпадают.
Кстати, математическое доказательство этого факта в ОТО занимает несколько страниц, исписанных формулами тензорного анализа. Поэтому объяснение "на пальцах" невозможно.