Загадочное обменное взаимодействие
Как обменное взаимодействие объяснить "на пальцах"? Возможно ли это?
Обычно считается, что обменное взаимодействие, это чисто квантовый эффект, который не имеет никаких аналогов в классической физике. И это так. Поэтому считается, что человеку невозможно объяснить природу обменного взаимодействия без знаний математики и квантовой механики.
Сейчас мы попробуем здесь без всякой математики объяснить, почему магнитные моменты парамагнитных атомов ферромагнетиков и антиферромагнетиков выстраиваются в том или ином порядке. Допустим, мы хотим объяснить это человеку, который мало разбирается в квантовой физике и в математике. Мы приведем даже некоторую механическую аналогию обменного взаимодействия с обычными шестеренками.
Но сначала, в этом разделе мы кратко рассмотрим основные свойства обменного взаимодействия.
Общие сведения об обменном взаимодействии
Обменное взаимодействие, это чисто квантовое явление взаимодействия двух тел, которые имеют моменты вращения. Грубо говоря, два достаточно близко расположенных друг к другу тела имеют разную энергию взаимодействия в зависимости от того, как они вращаются, в одну сторону или в разные стороны.
Например, энергия двух глобусов, вращающихся в одном направлении, не равна энергии этих же двух глобусов, которые с теми же самыми скоростями вращаются в противоположные направления. В классической механике эти энергии в точности равны друг другу. А в квантовой механике на уровне элементарных частиц, система из двух элементарных частиц имеет разные энергии в зависимости от взаимного направления их спинов (моментов вращения).
Это приводит к тому, что системе двух элементарных частиц более выгодно или перейти в состояние с одинаково направленными спинами или в состояние с противоположно направленными спинами. А с направлением спинов элементарных частиц связано направление магнитных моментов частиц. Поэтому в одних случаях в парамагнитных кристаллах магнитные моменты атомов выстраиваются в одном направлении (ферромагнитное упорядочение), в других случаях в противоположных направлениях ближайших соседних атомов (антиферромагнитное упорядочение), и в третьих случаях получаются другие разные сложные взаимные направления магнитных моментов ближайших соседних атомов.
Обменное взаимодействие и магнитное взаимодействие
Обратите внимание, что обменное взаимодействие никак не связано с магнетизмом и не имеет никакого отношения к магнитным явлениям. В том смысле, что обменное взаимодействие существует независимо от существования магнитного взаимодействия, и магнитное взаимодействие никак не влияет на обменное взаимодействие. Например, если мы рассмотрим две элементарные частицы, которые имеют спины и не имеют магнитных моментов, то обменное взаимодействие между ними будет точно такое же, как и между такими же элементарными частицами, у которых есть и такие же спины и магнитные моменты.
Обменное взаимодействие выстраивает в регулярный (или хаотический) порядок спины парамагнитных атомов в твердых телах. А так как направления спинов определяют направления магнитных моментов парамагнитных атомов, то получается, что обменное взаимодействие в качестве побочного эффекта выстраивает в твердых телах и направления магнитных моментов парамагнитных атомов. И таким образом, обменное взаимодействие оказывает существенное влияние на магнитные свойства всех парамагнетиков.
Так как магнитный порядок охватывает макроскопические объемы твердого тела, то такие явления, как ферромагнетизм, это квантовые явления, которые проявляют себя в макромире. К другим макроскопическим квантовым явлениям относятся, например, сверхпроводимость и сверхтекучесть. Именно поэтому неверно утверждать, что квантовая физика изучает только явления микромира.
Энергетический баланс обмена и магнетизма
С точки зрения магнитных явлений, ферромагнитный порядок расположения магнитных моментов является энергетически невыгодным. Минимуму энергии магнитостатического взаимодействия соседних парамагнитных атомов соответствует антиферромагнитное упорядочение, когда магнитные моменты ближайших соседних парамагнитных атомов направлены противоположно. Но обменное взаимодействие, это гораздо более сильное взаимодействие, по сравнению с магнитостатическим взаимодействием магнитных моментов. Поэтому, если ферромагнитное упорядочение более выгодно по сравнению с антиферромагнитным упорядочением, то это ферромагнитное упорядочение и реализуется, не смотря на то, что получается проигрыш по магнитостатической энергии.
С другой стороны, обменное взаимодействие, это короткодействующее взаимодействие, то есть обмен, это гигант с короткими руками. Обменное взаимодействие с увеличением расстояния падает практически по экспоненте. Поэтому обменное взаимодействие между ближайшими соседними атомами на порядок и более чем на порядок больше, чем обменное взаимодействие через один атом. А обменное взаимодействие через один атом, в свою очередь, еще на порядок и более чем на порядок больше, чем обменное взаимодействие между следующими соседями.
А магнитостатическое взаимодействие между магнитными моментами уменьшается с расстоянием по степенному закону. Магнитостатическое взаимодействие магнитных моментов, это дальнодействующее взаимодействие (слабый карлик с длинными руками). Это приводит к тому, что на больших расстояниях однородное упорядочение магнитных моментов нарушается. Поэтому ферромагнитный образец разбивается на систему магнитных доменов с однородной намагниченностью в объеме доменов и неоднородной намагниченностью на тонких границах между доменами.
Такое распределение намагниченности в ферромагнетиках приводит к сильному снижению энергии магнитостатического взаимодействия, так как намагниченности доменов направлены в разные стороны. А проигрыш в обменном взаимодействии получается совсем небольшим, так как доменные границы с неоднородной намагниченностью занимают небольшой объем.
Модель жестких шестеренок на параллельных осях
Аналогия с антиферромагнетиком
Допустим, у нас имеются два вертикальных жестких стержня и на эти стержни жестко посажены две одинаковые шестеренки с зубцами по внешним окружностям шестеренок. Если состыковать друг с другом шестеренки такой системы, то они смогут вращаться только в разных направлениях. Соответственно, и обе оси, на которые посажены шестеренки, тоже могут вращаться только в разные стороны.
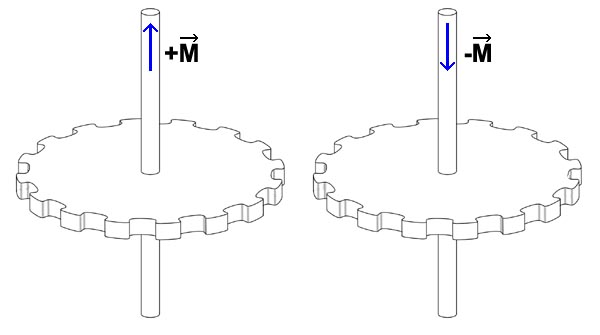
Причем, не важно, в каком конкретном направлении вращается первая шестеренка, по часовой стрелке или против часовой стрелки. Вторая шестеренка подстраивается под вращение первой шестеренки и вращается всегда в противоположном направлении.
Эта простая аналогия с жестко посаженными на ось шестеренками уже является неплохой аналогией антиферромагнитного упорядочения магнитных моментов парамагнитных атомов в антиферромагнетиках. Например, длинная цепочка таких шестеренок является аналогом одномерного антиферромагнитного упорядочения.

Если вся эта цепочка шестеренок равномерно заряжена, например, отрицательным электрическим зарядом, то вращение каждой шестеренки создает магнитный момент. И мы получаем систему чередующихся магнитных моментов, с разнонаправленными магнитными моментами ближайших соседей. Вся система в целом будет иметь нулевой суммарный магнитный момент.
Эти жестко посаженные на ось шестеренки являются не только аналогам одномерной модели антиферромагнетика, но и аналогом двумерной модели антиферромагнетика с шахматным магнитным порядком.

Аналогия с ферритом
На этой модели жестко посаженных шестеренок можно также объяснить и магнитное упорядочение ферритов (ферримагнетиков). Как известно, феррит, это не ферромагнетик, а антиферромагнетик, у которого магнитные моменты магнитных подрешеток в кристалле не компенсируют друг друга. Поэтому ферриты, как и ферромагнетики, могут находиться в состоянии постоянного магнита.
Причем в слабых внешних магнитных полях и при низких частотах этих полей, поведение ферритов ничем не отличается от поведения ферромагнетиков. Например, у ферритов такой же характер петли гистерезиса, как и у ферромагнетиков при перемагничивании в слабом внешнем магнитном поле с низкой частотой.
Аналогией феррита в одномерном случае может служить, например, цепочка чередующихся шестеренок двух разных диаметров. Соответственно, эти шестеренки будут иметь разные заряды и поэтому разные по величине магнитные моменты. Из-за этого полной компенсации магнитных моментов всех шестеренок не произойдет, и такая система заряженных шестеренок при вращении шестеренок будет иметь ненулевой суммарный магнитный момент.

Точно также, эти жестко посаженные на ось шестеренки разных диаметров являются не только аналогами одномерных моделей ферритов, но и двумерными моделями некомпенсированных антиферромагнетиков с шахматным порядком.

Переход парамагнетика в антиферромагнитное состояние
При нагревании любого антиферромагнетика, он переходит в парамагнитную фазу. Иногда ошибочно говорят, что он становится парамагнетиком. Это не совсем правильно, так как любой антиферромагнетик, это и есть уже парамагнетик, как и любой ферромагнетик или феррит. Просто парамагнетик может при низких температурах пройти через фазовый переход и оказаться в одном из магнитозамороженных состояний.
Магнитозамороженными состояниями могут быть магнитоупорядоченные состояния, такие, как, например, ферромагнитное состояние парамагнетика или антиферромагнитное состояние парамагнетика и другие. А могут быть и состояния с неупорядоченной магнитной структурой (спиновые стекла). Это такая же аналогия, как и переход жидкости в твердое состояние. При таком фазовом переходе получается или упорядоченное состояние кристалла или неупорядоченная аморфная структура.
Если мы считаем, что при нагревании кристалла расстояния между его атомами увеличиваются, то при увеличении расстояния между шестеренками, они уже не будут цепляться друг за друга. Исчезнет корреляция вращений шестеренок, и дальний магнитный порядок будет разрушен. Под действием высокой температуры магнитные моменты в атомах начинают беспорядочно менять своё направление по времени. Эти беспорядочные изменения никак не зависят от таких же беспорядочных изменений в соседних атомах кристаллической решетки. То есть при такой высокой температуре кристаллический порядок ещё существует, а вот магнитного порядка уже нет.
Аналогом уменьшения температуры в модели с шестеренками будет уменьшение расстояния между шестеренками до такого состояния, когда хаотично меняющие направление вращения шестеренки состыковываются друг с другом. При этом каждая шестеренка перестает хаотично менять направление своего вращения. В цепочке или в плоскости шестеренок устанавливается дальний магнитный порядок.
Недостатки аналогии с жестко посаженными шестеренками
Но вот трехмерные модели антиферромагнетиков с помощью жестко посаженных шестеренок создать уже не получится. Как известно, у обычных полностью скомпенсированных антиферромагнетиков в трехмерных кристаллах два основных вида магнитного порядка:
- Объемный шахматный порядок, когда шесть ближайших соседей по осям x, y и z имеют противоположно направленный магнитный момент, а 8 ближайших соседей по диагоналям имеют такой же магнитный момент.
- Послойный порядок, когда чередуются плоские слои с одинаково направленными магнитными моментами в каждом слое, но противоположно направленными магнитными моментами в соседних слоях.
Ни тот, ни другой порядок не получается моделировать с жестко посаженными на оси шестеренками.
И, конечно же, аналогия с жестко посаженными шестеренками никак не моделирует ферромагнитный порядок и не моделирует фазовые переходы между ферромагнитным и антиферромагнитным порядком.
Хитро посаженные шестеренки
Теперь посадим шестеренку на ось хитрым способом. Сделаем, так, чтобы ось всегда вращалась в строну противоположную вращению шестеренки. Кстати, технически это возможно. Для этого надо расширить внутреннее отверстие шестеренки и нарезать там зубчики. На оси тоже нарезать зубчики, а между осью и внутренним отверстием шестеренки вставить еще одну маленькую шестеренку. Нетрудно убедиться, что в такой конструкции большая шестеренка и ось будут всегда вращаться в разные стороны.
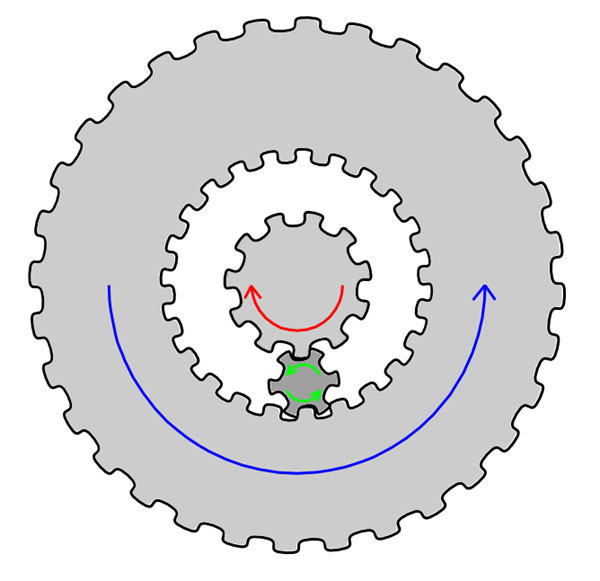
Для устойчивости всей конструкции можно взять не одну маленькую шестеренку, а три маленькие шестеренки и посадить их на три жестко закрепленные оси. Эти три маленькие оси должны быть жестко закреплены и не вращаться, а сами маленькие шестеренки должны свободно вращаться на этих трех маленьких осях, как показано на рисунке ниже.
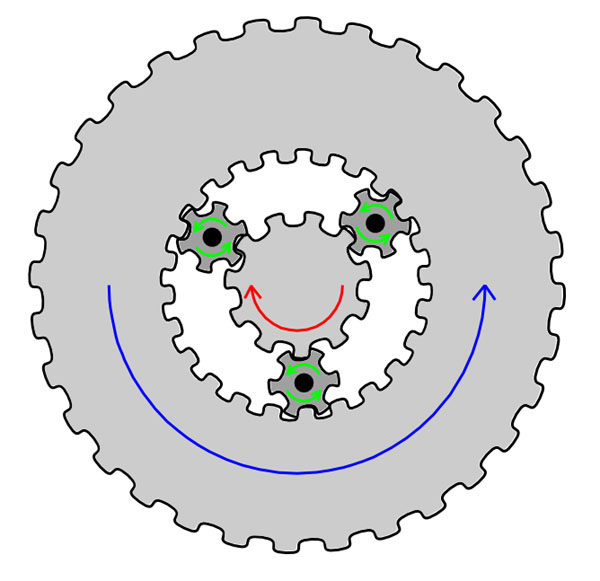
Нам эти технические подробности сейчас не принципиальны. Для нас главное, что мы теперь будем рассматривать системы и с жестко посаженными шестеренками и с хитро посаженными шестеренками. А технические подробности пригодятся, если кто-то захочет реально сконструировать эти модели и покрутить их.
И, кстати, теперь мы будем считать, что у нас электрически заряжены не шестеренки, а только стержни, на которые они жестко или хитро посажены. То есть магнитные моменты создаются только вращением заряженных стержней.
Понятно, что если состыковать между собой две хитро посаженные шестеренки, то стержни будут, как и раньше, вращаться в разные стороны. Но если состыковать между собой жесткую шестеренку и хитрую шестеренку, то стержни будут вращаться в одну и ту же сторону, туда, куда вращается жестко посаженная шестеренка.
Значит, чтобы сформировать ферромагнитную цепочку, надо чередовать жесткие и хитрые шестеренки. Для плоской модели ферромагнетика надо чередовать жесткие и хитрые шестеренки в шахматном порядке.
А если стержни у нас длинные, то мы насаживаем на них еще несколько плоских этажей шестеренок в таком же шахматном порядке, как в первой плоскости и получаем трехмерную модель ферромагнетика. Но это, конечно, не совсем правильная модель трехмерного ферромагнетика. Дело в том, что обменное взаимодействие изотропное, не зависит от того, вдоль какой прямой линии направлены спины. А у нас если оси шестеренок развернуть на 90 градусов, то стыковка шестеренок пропадает.
Можно легко придумать систему шестеренок в вертикальной плоскости, которые состыковывают между собой шестеренки из разных плоскостей. Для ферромагнитной структуры потребуются по две шестеренки, которые крутят соответствующие соседние шестеренки на разных соседних этажах. А для антиферромагнитной трехмерной структуры шахматного типа потребуется только одна шестеренка на каждую пару соседних шестеренок с разных этажей и нужно будет распилить все стержни по размеру этажей, чтобы соосные стержни соседних этажей могли вращаться в разные стороны.
Но, тем не менее, у обычных шестеренок нет шаровой симметрии, поэтому трехмерные модели обменного взаимодействия с обычными шестеренками получаются притянутыми "за уши" и уже не такими красивыми, как одномерные и двухмерные модели.
Переходы между ферромагнетиками и антиферромагнетиками
Зависимость обменного взаимодействия от расстояния
Один и тот же парамагнетик может находиться в разных магнитозамороженных состояниях. Иногда такие состояния связаны с разными кристаллическими структурами вещества. Например, такой вид стали (соединение железа с углеродом), как α-железо, это ферромагнетик (а точнее, феррит), а γ-железо, это антиферромагнетик. При этом альфа- и гамма-железо имеют разные кристаллические решетки. У α-железа объемноцентрированная кубическая решетка, а у γ-железа гранецентрированная кубическая кристаллическая решетка.
Часто встречаются и такие случаи, когда один и тот же парамагнетик при одной температуре имеет одну магнитоупорядоченную структуру, а при другой температуре имеет другую магнитоупорядоченную структуру. При этом кристаллическая решетка парамагнетика не меняется при таком фазовом переходе между разными магнитоупорядоченными состояниями.
Изменения, допустим, ферромагнитной структуры на антиферромагнитную структуру и обратно происходит за счет того, что обменное взаимодействие зависит от расстояния между атомами в кристалле. При изменении температуры меняются эти межатомные расстояния. В альфа-железе и гамма-железе тоже разные расстояния между ближайшими атомами железа, поэтому между парамагнитными атомами получается разное обменное взаимодействие в состоянии α-железа и γ-железа.
Разные другие магнитные структуры тоже показывают зависимость от температуры. Например, спиральные магнитные структуры сворачиваются или разворачиваются в зависимости от того, увеличивается или уменьшается температура. В неупорядоченных магнитных структурах типа спинового стекла при изменении температуры могут менять своё направление магнитные моменты в огромных кластерах.
Обменное взаимодействие зависит от расстояния между атомами знакопеременно. То есть при одном расстоянии между парамагнитными атомами будет энергетически выгодно одинаковые направления спинов в этих атомов, а при другом расстоянии между этими атомами минимуму энергии будет соответствовать противоположные направления спинов этих атомов. И если постепенно увеличивать расстояние между атомами, то будет поочередно то выгодно ферромагнитное направление спинов, то выгодно антиферромагнитное направление спинов. И, соответственно, магнитные моменты этих атомов, то будут направлены в одну сторону, то в противоположные стороны. И эти изменения взаимных направлений магнитных моментов будут меняться в зависимости от расстояния между атомами не так строго периодически, как, например, меняются синусы и косинусы, а квазипериодически.
Почему у обменного взаимодействия такое интересное поведение, это объясняется в самом последнем разделе этой статьи.
Пирамидка шестеренок
Такое поведение обменного взаимодействия в зависимости от расстояния мы будем моделировать не одной шестеренкой на оси, целой пирамидкой шестеренок разного диаметра. Шестеренки нужно надевать на ось по принципу детской пирамидки, сначала шестеренка с самым большим диаметром, потом поменьше и т.д. У нас в пирамидке жесткие и хитрые шестеренки будут идти поочередно. Допустим, сначала идет жесткая шестеренка, потом хитрая, потом опять жесткая, затем снова хитрая и т.д.
Мы будем пренебрегать квазипериодичностью зависимости обменного взаимодействия от расстояния. Пусть от расстояния всё зависит строго периодично. Поэтому диаметры шестеренок будут уменьшаться по линейному закону.
Соседние пирамидки будут состыковываться так, что одна из пирамидок стоит нормально, как детская игрушка, а другая пирамидка перевернутая. Так что пирамидки могут состыковываться между собой на разных расстояниях между осями. (Считаем, что оси можно перемещать не только по направлению друг к другу, но вверх-вниз.)
Если в двух соседних пирамидках состыковались друг с другом жесткие шестеренки одной пирамидки с жесткими шестеренками другой пирамидки, а хитрые шестеренки одной пирамидки с хитрыми шестеренками другой пирамидки, то оси этих пирамидок вращаются противоположно друг другу. Это расстояние между осями пирамидок соответствует антиферромагнитному обменному взаимодействию. А если у двух соседних пирамидок состыковались друг с другом жесткие шестеренки обоих пирамидок с хитрыми шестеренками обоих пирамидок, то оси этих пирамидок вращаются в одинаковом направлении. Это расстояние между осями пирамидок соответствует ферромагнитному обменному взаимодействию.
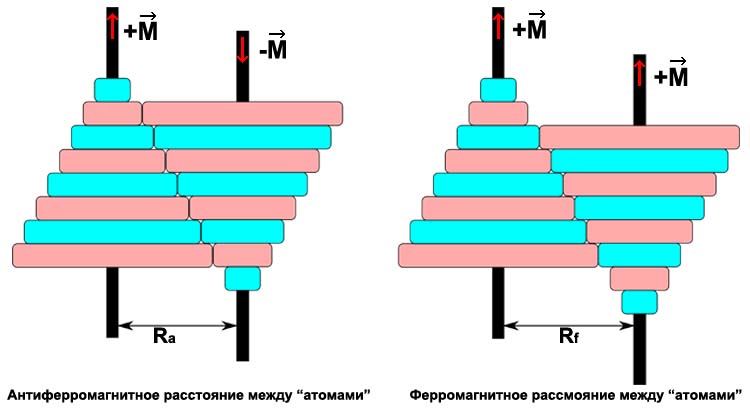
При одинаковом постепенном изменении всех расстояний между осями пирамидок в цепочке пирамидок или на плоскости мы получаем аналог фазовых температурных переходов между ферромагнитным и антиферромагнитным порядками.
Немного квантовой механики
Вот так с помощью модели шестеренок примерно, "на пальцах", можно объяснить, как работает обменное взаимодействие
А теперь для тех, кто немного знаком с квантовой физикой и квантовой механикой, расскажем еще кое что из того, откуда берется обменное взаимодействие, и почему у обменного взаимодействия нет аналога в классической механике.
Магнитный момент парамагнитного атома в кристалле обусловлен магнитными моментами неспаренных электронов, которые сидят на недостроенных внутренних электронных оболочках этого атома. А все спаренные электроны в атоме взаимно компенсируют магнитные моменты друг друга. Электроны на внешней недостроенной электронной оболочке атома спариваются за счет химических связей. А в металлах эти электроны с недостроенной внешней оболочки свободно перемещаются по всему кристаллу, то есть не имеют хорошей пространственной локализации.
Для простоты допустим, что в парамагнитном атоме на внутренней оболочке находится только один неспаренный электрон. Этот электрон достаточно хорошо локализован возле атома в яме потенциальной энергии. Поэтому амплитуда волновой функции такого электрона будет быстро радиально убывать по экспоненте. И, кроме того, на эту экспоненту будет наложена знакопеременная радиальная функция типа обобщенных полиномов Лягерра.
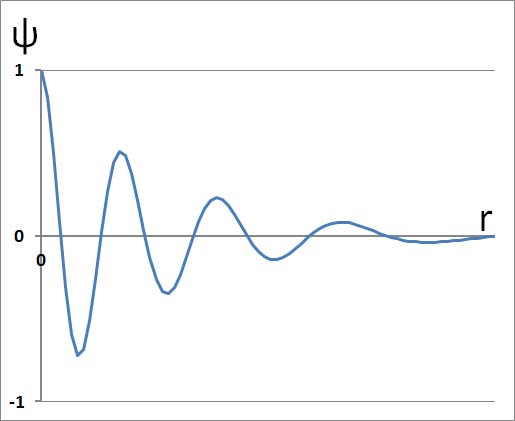
Такая задача в квантовой механике не имеет точного аналитического решения для амплитуды волновой функции, так как в классической механике эта задача соответствует неинтегрируемым дифференциальным уравнениям для задачи многих тел в гравитационном (или кулоновском) поле. Точное решение в виде формулы имеется только для электрона в атоме водорода. Но на качественном уровне зависимость от радиуса амплитуды волновой функции электрона на внутренней электронной оболочке в атоме с большим числом электронов ведет себя качественно примерно также, как и амплитуда волновой функции электрона в атоме водорода.
Направление спина этого неспаренного электрона влияет только на знак амплитуды волновой функции. Поэтому на наблюдаемые величины для одного электрона направление спина этого электрона не оказывает никакого влияния. Плотность вероятности пространственного распределения местонахождения этого электрона вычисляется как квадрат модуля этой волновой функции, то есть плотность вероятности не зависит от знака амплитуды волновой функции.
Но всё меняется, если рядом находится еще один парамагнитный атом, допустим, точно такой же с одним неспаренным электроном на внутренней оболочке. В этом случае "хвосты" амплитуд волновых функций этих электронов начинают накладываться друг на друга.
Могут наложиться друг на друга преимущественно положительные участки амплитуды первого электрона на преимущественно положительные участки амплитуды второго электрона, а преимущественно отрицательные участки амплитуды первого электрона на преимущественно отрицательные участки амплитуды второго электрона. А могут, и наоборот, наложиться друг на друга преимущественно положительные участки каждого электрона на преимущественно отрицательные участки каждого электрона.
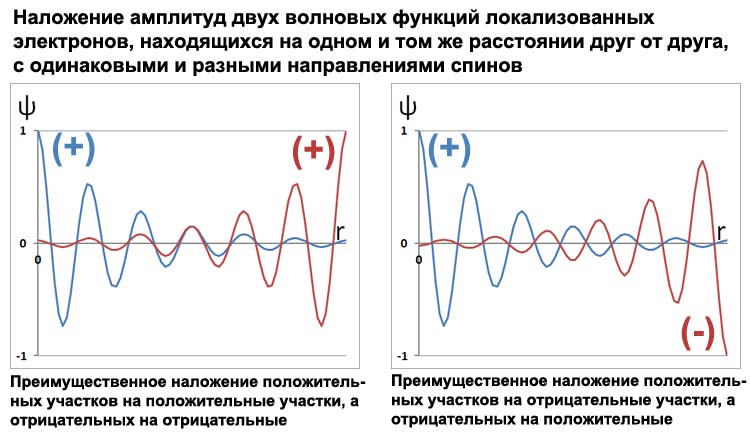
Как именно произойдет такое наложение, зависит не только от расстояния между парамагнитными атомами, но и от взаимных знаков амплитуд волновых функций этих неспаренных электронов на недостроенных внутренних оболочках атомов. То есть зависит от взаимного направления спинов этих электронов. Если оба спина электрона меняются на противоположные спины, то меняются знаки у обеих амплитуд, и это не влияет на взаимное наложение амплитуд. Но если меняется направление спина только у одного электрона, то сразу же меняется характер взаимного наложения амплитуд. Например, если преимущественно положительные участки накладывались на друг на друга, и преимущественно отрицательные участки тоже накладывались друг на друга, то смена знака приведет к тому, что накладываться друг на друга будут отрицательные и положительные участки.
Это, конечно, очень утрированные рассуждения. Эти рассуждения просто показывают, как электроны в соседних атомах "чувствуют" взаимные направления спинов друг друга.
Если всё делать по честному, то надо решать стационарное уравнение Шредингера для системы двух частиц в двух потенциальных ямах, которые соответствуют энергетическим ямам электронов на внутренней электронной оболочке атома. Решением такого уравнения будет набор общих волновых функций, зависящих от координат двух электронов. Каждой такой волновой функции будет соответствовать свой энергетический уровень.
Но если в такую задачу внести учет спинов электронов, то каждый энергетический уровень, найденный для бесспиновых частиц, раздваивается на два энергетических уровня. Один из которых соответствует одинаковому направлению спинов, а другой разным направлениям спинов. Такое раздвоение энергетических уровней происходит из-за того, что для разных взаимных направлений спинов в решении получаются две разные амплитуды волновых функций. А почему эти волновые функции, зависящие сразу от координат двух электронов, должны быть обязательно разными, было рассказано выше при рассмотрении наложения амплитуд волновых функций невзаимодействующих электронов.
Если увеличивать расстояние между атомами, то эти раздвоенные уровни будут менять своё положение относительно друг друга. Поэтому при одних расстояниях основным состоянием системы будет состояние с одинаково направленными спинами, а при других расстояниях основным состоянием системы будет состояние с противоположным направлением спинов.
P.S.
Вопрос: А почему обменное взаимодействие называется обменным? Что там с чем меняется?
Ответ: При решении задачи о двух частицах в двух потенциальных ямах с барьером конечной высоты и конечной ширины между ямами, получается, что эти ямы (атомы) могут обмениваться своими
частицами за счет квантового туннелирования.