Простая задача о взвешивании монет была описана в этой статье. А сейчас мы рассмотрим одну из самых удивительных задач о взвешивании монет. Эта задача любого человека может поставить в тупик. Красивое решение этой задачи покажет нам всю мощь математики.
Сначала мы сформулируем эту задачу в самом общем виде. А потом сильно упростим её и сначала дадим решение для очень упрощенного варианта. Это нужно, чтобы понять главную идею решения задачи. Поняв главную идею решения, мы начнем постепенно усложнять эту задачу и доведём её до общего вида.
Общая задача
Пусть имеется N мешков с монетами. Все эти монеты на вид ничем не отличаются друг от друга. Это или настоящие монеты или какой-нибудь один сорт фальшивых монет. В каждом мешке находятся монеты только одного какого-нибудь вида, то есть или настоящие или один из сортов фальшивых. Нам известно, сколько весит одна монета каждого сорта. То есть известен вес настоящей монеты и веса всех сортов фальшивых монет. Неизвестно в каких именно мешках находятся настоящие монеты, а в каких мешках находятся фальшивые монеты.
Задача: Как ОДНИМ взвешиванием определить, в каких мешках находятся настоящие монеты, а в каких мешках находятся какие сорта фальшивых монет? Весы обычные, которые показывают вес, например, в граммах.
Будем считать, что все мешки достаточно большие, то есть в мешках находится достаточное количество монет, чтобы брать оттуда любое количество монет для взвешивания.
Заметим, что, в общем случае, фальшивые монеты не обязательно должны быть легче, чем настоящие монеты. Например, может быть, что всего 7 сортов монет со следующими весами в граммах: 4, 5, 8, 9, 10, 13 и 16. При этом, например, настоящая монета имеет вес 10 грамм, а все остальные веса (4, 5, 8, 9, 13 и 16) соответствуют фальшивым монетам.
Кроме того, у нас не обязаны все 7 сортов этих монет обязательно присутствовать в каких-нибудь мешках. Возможно, что во всех N мешках находятся только одни настоящие монеты, или во всех N мешках находятся только фальшивые монеты, например, с весом 9 грамм. Или могут быть любые более сложные ситуации, когда часть мешков занята одним сортом монет, часть мешков другим сортом монет и т.д. И нам неизвестно в каком порядке чередуются мешки с этими монетами.
Попробуйте сейчас не читать дальше, а попытаться решить эту задачу. Или хотя бы подумайте минут пять, чтобы придумать идею решения такой задачи.
Подумали? Тогда читайте дальше.
Если эту задачу сразу сформулировать в таком общем виде, то большинство людей, пытаясь её решить, приходят к выводу, что это невозможно вот так одним взвешиванием определить весь расклад монет по всем мешкам. И, тем не менее, за одно взвешивание можно определить всё распределение всех сортов монет по всем N мешкам.
Очень сильно упрощенная задача
Максимально упрощенная задача выглядит так. Имеется N мешков с монетами. Во всех мешках, кроме, возможно, одного мешка, находятся настоящие монеты. И, возможно, в одном мешке находятся фальшивые монеты. Нужно с помощью одного взвешивания найти мешок с фальшивыми монетами, если таковой имеется.
Пусть для определенности настоящая монета весит, например, 10 грамм, а фальшивая весит 9 грамм, то есть на 1 грамм легче. И так как мы математики, то, естественно, что у нас все мешки пронумерованы числами от 1 до N.
При N=1 задача решается тривиально. Берем одну монету из мешка и взвешиваем её. Если она весит 10 грамм, то в мешке настоящие монеты. А если она весит на 1 грамм меньше, то это мешок с фальшивыми монетами.
Для N=2 очень легко можно сообразить, что из первого мешка нужно взять одну монету, а из второго мешка нужно взять 2 монеты. Если во всех двух мешках только настоящие монеты, то эти три монеты вместе будут весить 30 грамм. Если первый мешок с фальшивыми монетами, то вес будет 9 + 10 + 10 = 29 грамм, то есть на 1 грамм меньше. Если фальшивые монеты во втором мешке, то вес будет 10 + 9 + 9 = 28 грамм, то есть на 2 грамма меньше, чем надо.
Для N=3 поступаем также. Из мешка номер 1 берем 1 монету, из мешка номер 2 берем 2 монеты, и из мешка номер 3 берем 3 монеты. Итого взяли 6 монет. Если они все настоящие, то их общий вес будет 60 грамм. Если их вес на 1 грамм меньше, то фальшивые монеты в 1-м мешке, если на 2 грамма меньше, то во 2-м мешке, и если на 3 грамма меньше, то фальшивые монеты в 3-м мешке.
Итак, для общего числа мешков N, из каждого мешка берем число монет равное номеру мешка. И затем смотрим, на сколько грамм вес взятых монет оказался меньше того веса, который был бы, если бы все монеты были бы настоящие. Если полный вес взятых монет оказался ожидаемым весом для настоящих монет, то есть меньше на 0 грамм, то фальшивых монет нет. Если вес оказался меньше на n грамм, чем ожидаемый, то фальшивые монеты находятся в мешке номер n.
Ожидаемый общий вес взятых из мешков монет в случае только настоящих монет вычисляется по формуле суммы арифметической прогрессии:
10 + 20 + 30 + ... + 10n + ... +10N = 10N(N+1)/2
В общем случае, если настоящая монета весит g0 грамм, то ожидаемый вес взятых монет будет
g0N(N+1)/2
Если фальшивая монета весит g грамм, то разница в весе двух монет будет Δg = g0 - g. Тогда полный вес G всех взятых из мешка монет будет
G = g0N(N+1)/2 - nΔg
Отсюда находим номер мешка
n = (g0N(N+1)/2 - G)/Δg
Например, если N=8, настоящая монета весит 10 грамм, фальшивая весит 16 грамм, а вес всех взятых из мешков монет получился равным 390 грамм, то
n = (10*8*(8+1)/2 - 390)/(10-16) = (360 - 390)/(-6) = 5
То есть тяжелыми фальшивыми монетами по 16 грамм наполнен мешок номер 5.
Чуть более сложная задача
Мы специально очень подробно рассмотрели решение очень сильно упрощенной задачи, чтобы Вы поняли главную идею решения сложной задачи: нужно искать такую комбинацию взятых из мешков монет, чтобы их общий вес однозначно указывал на распределение монет разных сортов по всем мешкам.
Чуть усложним нашу сильно упрощенную задачу из предыдущего раздела. Пусть теперь среди всех мешков с монетами может быть не один мешок с фальшивыми монетами, а R мешков с фальшивыми монетами одного и того же типа. При этом, в общем случае, 0 ≤ R ≤ N, то есть фальшивых монет может и не быть совсем, и может быть так, что во всех мешках только одни фальшивые монеты. И, разумеется, если R больше нуля и меньше N, то нам неизвестно, как распределены фальшивые монеты по номерам мешков. Это распределение и нужно вычислить.
Для N=1 всё также, как и в предыдущем случае. Берем одну монету и взвешиваем её. Если она весит 10 грамм, то в мешке настоящие монеты. Если она весит, например, 9 грамм, то в мешке фальшивые монеты.
Для N=2 тоже, как и в упрощенной задаче, из первого мешка берем одну монету, а из второго две монеты. Если вес оказался меньше 30 грамм на 3 грамма, то это означает, что фальшивые монеты сразу в двух мешках.
Для N=3 уже не получается из третьего мешка взять только три монеты, так как в этом случае если общий вес взятых монет окажется меньше на 3 грамма, то непонятно, где фальшивые монеты, в двух первых мешках или в третьем мешке. Но если из третьего мешка взять 4 монеты, то всё получается нормально. В этом случае по общему весу можно отличить ситуацию с фальшивыми монетами в двух первых мешках или в третьем мешке.
Если для N=3 вес взятых монет оказался меньше на 5 грамм, то это означает, что фальшивые монеты в первом и третьем мешках (1 + 4 = 5). Если вес оказался меньше на 6 грамм, то фальшивые монеты во втором и третьем мешках (2 + 4 = 6). Наконец, если вес оказался меньше на 7 грамм, то фальшивые монеты находятся во всех трех мешках (1 + 2 + 4 = 7).
Итак, для N=3 любое уменьшение веса от ожидаемых 70 грамм от 0 грамм до 7 грамм однозначно указывает на распределение настоящих и фальшивых монет по всем трем мешкам.
Для N=4 из четвертого мешка нужно уже взять 8 монет. Рассуждая, как выше, можно показать, что такое взятие монет из 4-х мешков однозначно определяет распределение настоящих и фальшивых монет по 4-м мешкам по уменьшению их общего веса от 150 грамм.
Когда во всех 4-х мешках только фальшивые монеты, вес взятых монет будет на 15 грамм меньше веса 150 грамм, который был бы, если бы это были бы только настоящие монеты. Поэтому для N=5 из 5-го мешка берем уже 16 монет.
Итак, получается, что, когда у нас может быть много мешков с одним и тем же сортом фальшивых монет, то брать монеты из мешков нужно уже не в порядке арифметической прогрессии, а в порядке геометрической прогрессии, удваивая взятое количество при переходе к следующему номеру мешка.

Число взятых из мешка монет kn связано с номером мешка n формулой
kn = 2(n-1)
Если бы мы были не математиками, а программистами, то мы бы пронумеровали мешки, начиная не от 1, а от 0, и тогда бы эта формула имела бы более простой вид.
Если в мешках все монеты только настоящие весом g0, тогда общий вес всех взятых монет будет
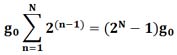
Если вес взятых монет оказался G, а разница между весом настоящей монеты g0 и весом фальшивой монеты g будет Δg = g0 - g, то число P, однозначно определяющее распределение монет по мешкам, будет вычисляться по формуле:
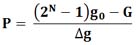
Чтобы по найденному числу P узнать распределение настоящих и фальшивых монет по мешкам, нужно число P записать в двоичной системе исчисления. Если смотреть на полученное двоичное число справа налево, то номера тех разрядов, где стоят единицы, будут соответствовать номерам тех мешков, где находятся фальшивые монеты. А номера тех разрядов, где стоят нули, будут соответствовать номерам тех мешков, где находятся настоящие монеты.
Например, пусть у нас имеется 10 мешков с монетами (N=10). Настоящие монеты весят 10 грамм, а фальшивые 9 грамм, то есть Δg = 1 грамм. Если бы все монеты были бы настоящие, то вес всех взятых монет был бы 10230 грамм. Но взвешивание показало вес взятых монет равным 10024 грамм. Отсюда находим распределительное число P = (10230 - 10024)/1 = 206.
Запишем число 206 в двоичной системе
206 = 11001110
Получается, что в первом мешке находятся настоящие монеты. Затем в трех мешках с номерами 2,3 и 4 находятся фальшивые монеты. В следующих двух мешках с номерами 5 и 6 находятся настоящие монеты. Затем в двух мешках с номерами 7 и 8 опять находятся фальшивые монеты.
А что же находится в мешках с номерами 9 и 10? В них находятся настоящие монеты. Дело в том, что, если в двоичной записи распределительного числа оказалось разрядов меньше, чем число N, то спереди все недостающие разряды нужно дополнить нулями.
206 = 0011001110
Действительно, число 206 можно записать как
206 = 0*29 + 0*28 + 1*27 + 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 1*21 + 0*20 =
= 0*512 + 0*256 +1*128 +1*64 +0*32 + 0*16 + 1*8 + 1*4 +1*2 +0*1
Отсюда хорошо видно, за счет каких мешков возникла разница в весе, и что за счет двух последних мешков разницы в весе не возникло.
Еще более сложная задача
Пусть теперь у нас не один вид фальшивых монет, а два вида фальшивых монет. Пусть для определенности настоящая монета весит 10 грамм, первый вид фальшивой монеты весит 9 грамм и фальшивая монета второго вида весит 8 грамм.
Для N=1 всё, по прежнему, очень тривиально. Берем из мешка одну монету и взвешиваем её.
А для N=2 взять из второго мешка 2 монеты уже не получится. Ведь если вес всех взятых монет окажется меньше на 2 грамма, чем был бы вес настоящих монет, то эта ситуация соответствует двум разным наборам монет. Так получается, если взяли одну фальшивую монету второго вида (легче на 2 грамма) из первого мешка и настоящие 2 монеты из второго мешка, а также, если из первого мешка взяли настоящую монету, а из второго мешка взяли две фальшивые монеты первого вида (легче на 1 грамм).
Получается, что для N=2 из 2-го мешка надо уже взять 3 монеты.
Рассуждая точно также, как в предыдущей задаче, мы приходим к выводу, что для N=3 из 3-го мешка надо взять 9 монет. Для N=4 из 4-го мешка нужно брать 27 монет.
Итак, когда у нас 3 вида монет (одна настоящая и два вида фальшивых), то из мешков надо брать число монет, которое соответствует последовательным степеням числа 3.

Число взятых из мешка монет kn связано с номером мешка n формулой
kn = 3(n-1)
Если в мешках все монеты только настоящие весом g0, тогда общий вес всех взятых монет будет
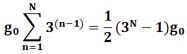
Введем понятие минимального шага между весами монет Δg = g0 - g1, где g0, это вес настоящей монеты, а g1, это вес ближайшей по значению фальшивой монеты. В нашем примере g0 = 10 грамм, а g1 = 9 грамм.
Обратите внимание, что понятие минимального шага между весами монет вводится только тогда, когда веса всех монет можно получить из веса настоящей монеты, отнимая (или прибавляя) от неё последовательно минимальные шаги между весами. Наш пример с весами монет 10, 9 и 8 грамм подходит под этот случай, так как g1 = g0 - Δg, и g2 = g1 - Δg. Если бы второй вид фальшивой монеты весил бы не 8 грамм, а, например, 7, то понятие минимального шага между весами ввести бы не получилось.
Если при взвешивании взятых из мешка монет, их вес оказался бы равен G, то распределительное число вычисляется по формуле
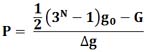
Это распределительное число нужно перевести в третичную систему исчисления и также посмотреть на него справа налево. Номера тех разрядов, где стоят нули, будут соответствовать номерам тех мешков, где находятся настоящие монеты. Номера тех разрядов, где стоят цифры 1, будут соответствовать номерам тех мешков, где находятся фальшивые монеты, которые отличаются весом от настоящих монет на один минимальный шаг между весами монет (g1 = g0 - 1*Δg). Номера тех разрядов, где стоят цифры 2, будут соответствовать номерам тех мешков, где находятся фальшивые монеты, которые отличаются весом от настоящих монет на 2 минимальных шага между весами монет (g2 = g0 - 2*Δg).
Обратите внимание, что в такой трактовке вес настоящей монеты должен быть или самым большим по сравнению с весами фальшивых монет или самым маленьким по сравнению с весами остальных монет. В последнем случае минимальный шаг Δg является отрицательным. И, соответственно, более тяжелые фальшивые монеты приводят к тому, что числитель формулы для вычисления распределительного числа P тоже становится отрицательным (если имеются фальшивые монеты).
Посмотрим пример.
Пусть фальшивые монеты имеют веса 8 грамм и 9 грамм, а настоящая монета весить 10 грамм. И пусть всего 6 мешков (N=6). Если бы все монеты были бы настоящие, то вес всех монет, взятых из 6 мешков, был бы 10*(36-1)/2 = 3640 грамм. Но допустим, реально их вес оказался только 3433.
Получаем распределительное число P = (3640-3433)/1 = 207. Запишем 207 в третичной системе:
207 = 021200
Здесь спереди числа в третичной системе сразу добавлен ноль, чтобы цифр в числе было столько же, сколько и число мешков N=6.
Смотрим на это третичное число справа налево и видим искомое распределение. В первых двух мешках с номерами 1 и 2 находятся настоящие монеты, в мешке номер 3 находятся фальшивые монеты, которые отличаются от настоящих монет на два минимальных шага, то есть с весом 8 грамм. В мешке номер 4 находятся фальшивые монеты, которые отличаются от настоящих на один минимальный шаг, то есть которые весят 9 грамм. Далее в мешке номер 5 снова находятся фальшивые монеты весом 8 грамм. И, наконец, в последнем 6-м мешке находятся настоящие монеты.
Действительно, число 207 можно представить как:
207 = 9*2 + 27*1 +81*2
Отсюда хорошо видно, что из 3-го мешка берутся 9 монет с недостатком в 2 грамма у каждой монеты, из 4-го мешка берутся 27 монет с недостатком в 1 грамм и из 5-го мешка 81 монета с недостатком в 2 грамма у каждой монеты.
Почти самая сложная задача
Теперь понятно, как будет решаться такая задача, когда фальшивых монет M видов и веса всех этих фальшивых монет отличаются от веса настоящей монеты на числа кратные минимальному шагу весов, причем веса фальшивых монет идут по порядку без пропусков.
Например, пусть настоящая монета весит 10 грамм. Пусть имеется еще M=4 вида фальшивых монет меньшего веса. Допустим, минимальный шаг веса составляет Δg = 1 грамм. Тогда фальшивые монеты весят gi = g0 - i*Δg. Здесь i, это номер вида монеты. То есть фальшивые монеты весят g1 = 9 грамм, g2 = 8 грамм, g3 = 7 грамм и g4 = 6 грамм.
Так как всего M + 1 = 5 видов всех монет, то берем из мешков число монет соответствующее степеням числа 5.

Разницу в весе между тем весом, который получился бы, если бы все монеты были бы настоящими и тем весом, который реально получился, делим на величину минимального шага. Полученное распределительное число записываем в 5-ричной системе исчисления. Добавляем спереди полученного числа нули, если число цифр в 5-ричном числе оказалось меньше, чем число мешков N. И получаем справа налево распределение монет по номерам мешков.
Номер разряда в 5-ричном числе справа налево совпадает с номером мешка, а цифра совпадает с номером i, который имеет монета. Причем, i = 0 соответствует настоящей монете, так как её вес g0 = g0 - 0*Δg, то есть i = 0. Цифра в 5-ричном числе показывает на сколько минимальных шагов отличается вес монеты в мешке от веса настоящей монеты.
Если все монеты в мешках только настоящие, то, в общем, случае вес всех выбранных монет будет
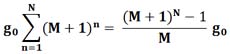
От этого веса нужно отнять реальный вес, полученный взвешиванием взятых монет, и разделить результат на минимальный шаг весов монет. Полученное число надо преобразовать в систему исчисления с основанием M+1. Тогда визуально мы увидим распределение монет по мешкам.
Обратите внимание, что, если M=9, то полученное число уже сразу находится в 10-ричной системе.
Финальная задача
Осталось решить только ещё два вопроса:
- Как быть если есть фальшивые монеты и весом меньше веса настоящих монет, и весом больше веса настоящих монет?
- Как быть, если веса всех фальшивых монет не распределены по порядку с кратностью отстройки равной минимальному шагу от веса настоящей монеты?
Для этого введем два нужных понятия:
- Базовая монета.
- Фиктивная монета.
Базовая монета
Базовая монета, это монета с самым наименьшим весом среди всех или с самым наибольшим весом среди всех монет.
У нас до сих пор, по умолчанию, в качестве базовой монеты выступала всегда настоящая монета. Но с точки зрения математики нет никакой разницы между настоящей монетой и фальшивой монетой. Мы в качестве базовой монеты можем взять и фальшивую монету, если её вес или самый большой среди всех монет или самый маленький среди всех монет.
Рассмотрим ещё раз пример из раздела для M=2. Пусть базовая монета (для i=0) будет фальшивая монета весом g0 = 8 грамм, для i=1 будет монета с весом g1 = 9 грамм, а для i=2 будет настоящая монета с весом g2 = 10 грамм.
Если во всех мешках были бы базовые монеты, то в том примере для N=6 вес всех взятых монет был бы 8*(36-1)/2 = 2912 грамм. Напоминаю, что в том примере реальный вес монет оказался 3433 грамма. Получается распределительное число P = (2912-3433)/(-1) = 521.
Переводим 521 в третичную систему:
521 = 201022
Мы получаем точно такой же результат распределения монет по мешкам, как и в том примере. Только теперь цифра ноль означает фальшивые монеты весом g0 = 8 грамм, цифра 2 означает настоящие монеты весом g2 = 10 грамм, а цифра один, как и раньше означает фальшивые монеты весом g1 = 9 грамм.
В том примере у нас получилось распределительное число 207. Для сравнения напишем здесь его третичный вид еще раз
207 = 021200
Сумма этих двух взаимных распределительных чисел будет
521 + 207 = 728 = 36 - 1
201022 + 021200 = 222222 = 1000000 - 0000001
В общем случае сумма двух взаимных распределительных чисел будет
(M+1)N - 1
Итак, если есть фальшивые монеты весом и больше и меньше настоящих монет, то весь алгоритм поиска распределений монет остается прежним, но только он теперь уже делается на базе базовой монеты, которая является или самой легкой монетой из всех или самой тяжелой.
Например, если настоящая монета весит 10 грамм, а фальшивые весят 9 грамм и 11 грамм, то в качестве базовой монеты можно выбрать или фальшивую монету весом 9 грамм или фальшивую монету весом 11 грамм.
Фиктивная монета
Будем называть фиктивной монетой такую монету, которой на самом деле в мешках не может быть, но присутствие которой формально учитывается в расчетах. Учет таких фиктивных монет не должен влиять на конечный результат.
Чтобы понять, как это работает рассмотрим еще раз пример для M=1 и для N=10, когда у нас была в качестве базовой настоящая монета весом g0 = 10 грамм, а фальшивая монета имела вес g1 = 9 грамм. В том примере у нас было N=10 мешков с монетами. Но мы точно знали, что третьей монеты тут быть не может, поэтому из мешков брали число монет равное степеням числа 2.
Допустим, что мы заранее не знаем, что второго вида фальшивых монет тут быть не может, и, на всякий случай, предполагаем, что в каких-то мешках могут быть ещё и монеты весом g2 = 8 грамм. Поэтому мы берем из мешков количество монет равное степеням числа 3.
В том примере у нас получилось распределительное число 206, которое записанное в двоичной системе дает следующее распределение монет по мешкам:
206 = 0011001110
В этой таблице указано, сколько монет надо взять из мешков, если это количество равно степеням числа 2 и степеням числа 3. Красным цветом выделены те мешки, которые содержат фальшивые монеты весом g1 = 9. Если сложить красные числа в строке, где стоят степени числа 2, то как раз и получится число 206. То есть 206 монет оказалось фальшивыми, и поэтому общий вес оказался не 10230 грамм, а 10024, что на 206 грамм меньше.

Поэтому если сложить вместе все красные числа в строке, где стоят степени числа 3, то мы тоже получим разницу в весе между весом монет, если бы они были все настоящие, и реальным весом взятых монет с учетом такого распределения фальшивых монет по мешкам. Это число получается равным 2955. Запишем это распределительное число в 3-чной системе исчисления:
2955 = 0011001110
И мы получаем точно такое же распределение по мешкам, как в случае, когда мы точно знали, что у нас только два вида монет, настоящие и один вид фальшивых. В 3-чной записи числа 2955 отсутствует цифра 2.
Предположим, что у нас в этом примере могут быть не только фальшивые монеты весом g2 = 8, но и фальшивые монеты с весами g3 = 7 и g4 = 6. Тогда представление распределительного числа в 5-чной системе исчисления тоже содержало бы только нули и единицы и выглядело бы как двоичное представление числа 206. Если 5-чное число 0011001110 представить в виде десятичного числа, то мы получим ту разницу в весе, которая будет, если брать из мешков число монет равное степеням числа 5.
Таким образом, эта последовательность нулей и единиц, 0011001110, является инвариантом, который будет получаться для любого числа основания M+1. Если мы выбираем из мешков число монет равное степеням числа M+1, а разницу в весе представляем в (M+1)-чной системе исчисления, то в нашем примере всегда получается последовательность 0011001110, которая соответствует реальному распределению монет по мешкам.
Обратите внимание, что фиктивные монеты не обязательно можно добавлять по минимальному шагу разницы в весе между базовой монетой и ближайшей к ней по весу. Например, в том же самом примере с настоящей монетой весом 10 грамм и фальшивой монетой весом 9 грамм, мы можем ввести фиктивную монету весом 9.5 грамм, а минимальный шаг сделать равным полграмма. То есть Δg=0.5, g0 = 10 грамм, g1 = 9.5 грамм и g2 = 9 грамм. В этом случае распределительное число P представленное в 3-чной системе исчисления будет выглядеть так:
0022002220
Отсутствие цифры 1, говорит о том, что в мешках нет монет весом g1 = 9.5 грамм. Цифры 2 показывают, в каких мешках содержатся монеты весом g2 = 9 грамм, а цифры 0 показывают в каких мешках содержатся настоящие монеты весом g0 = 10 грамм. Как видите, это распределение полностью совпадает с тем распределением, которое должно быть.
Окончательное решение
Итак, теперь мы можем решить очень общую задачу. Например, допустим у нас всего 7 сортов монет со следующими весами в граммах: 4, 5, 8, 9, 10, 13 и 16. При этом, например, настоящая монета имеет вес 10 грамм, а все остальные веса (4, 5, 8, 9, 13 и 16) соответствуют фальшивым монетам.
Если базовая монета будет монетой с весом g0 = 4 грамма, то можно заметить, что все эти веса можно получить с помощью применения формулы gi = g0 - i*Δg с минимальным шагом равным Δg = -1 грамм. Но при этом часть весов получаются фиктивными. Это g2 = 6, g3 =7, g7 = 11, g8 = 12, g10 = 14 и g11 = 15. Всего в сумме, реальных и фиктивных, получается 13 монет. Поэтому берем из мешков число монет равное степеням числа 13.
Разницу между весом, который был бы, если бы все монеты весили 4 грамма 4*(13N-1)/12 и реальным весом делим на минимальный шаг весов и получаем распределительное число P. Представим это P в 13-чной системе исчисления. Читая цифры этого числа справа налево, мы получаем распределение i-ых монет по номерам мешков.
Вот и всё.
P.S.
Вряд ли в жизни Вам когда-нибудь придется на практике взвешивать монеты в поиске мешков с фальшивыми монетами. А вот переводить числа в другие системы исчисления, возможно, когда-нибудь придется. И тогда
Вам пригодится этот Калькулятор конвертора систем исчисления.